Divisibility Rules Printable Sheet

The concept of divisibility rules is a fundamental aspect of mathematics, particularly in the realm of arithmetic. Understanding these rules is essential for students, educators, and professionals alike, as they facilitate the process of determining whether a number is divisible by another. In this article, we will delve into the world of divisibility rules, exploring their significance, applications, and providing a comprehensive printable sheet for reference.

Divisibility rules are a set of guidelines used to determine if a number can be divided evenly by another number. These rules are based on the properties of numbers and their relationships with each other. By applying these rules, individuals can quickly and accurately determine the divisibility of a number without having to perform lengthy calculations. The importance of divisibility rules lies in their ability to simplify mathematical operations, making them an indispensable tool in various fields, including science, technology, engineering, and mathematics (STEM).

The application of divisibility rules is not limited to academic settings; they are also used in everyday life. For instance, when shopping, individuals may need to determine if a certain quantity of items can be divided evenly among a group of people. In cooking, divisibility rules can be used to adjust ingredient quantities for a specific number of servings. Furthermore, in finance, understanding divisibility rules can help individuals manage their budgets and make informed decisions about investments.

Introduction to Divisibility Rules

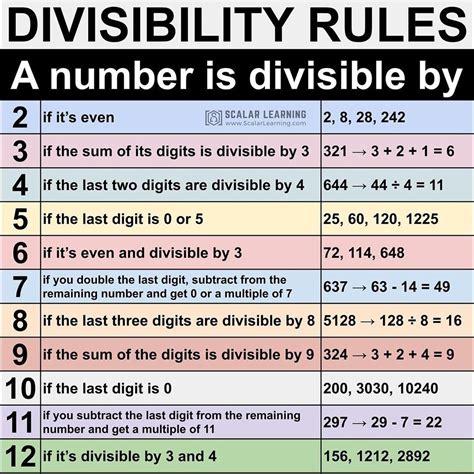
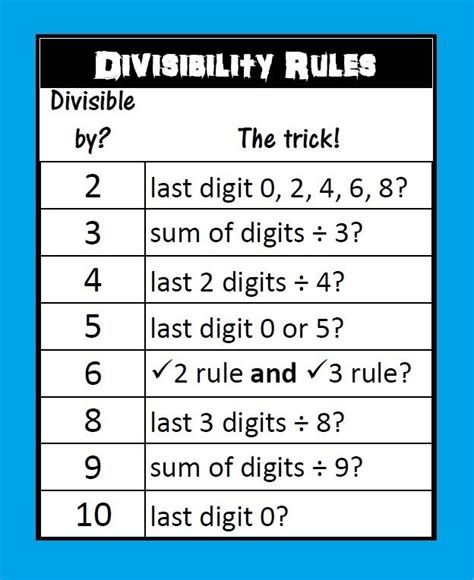
To understand divisibility rules, it is essential to familiarize oneself with the basic principles of arithmetic. The most fundamental divisibility rule is the rule of 1, which states that any number is divisible by 1. Other essential divisibility rules include the rules of 2, 3, 4, 5, 6, 7, 8, 9, and 10. Each of these rules has a unique characteristic that can be used to determine divisibility. For example, the rule of 2 states that if a number ends in 0, 2, 4, 6, or 8, it is divisible by 2.

Divisibility Rules for Specific Numbers

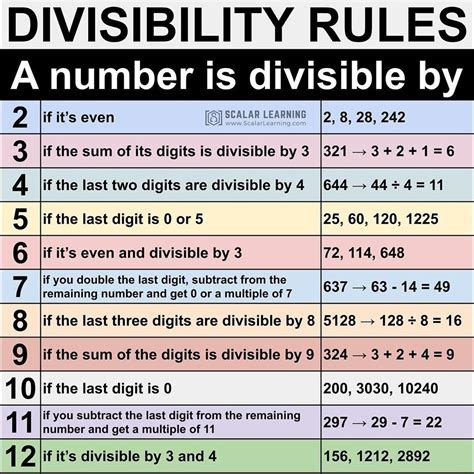
In addition to the basic divisibility rules, there are specific rules for certain numbers. The rule of 11, for instance, states that if the difference between the sum of the digits in the odd positions and the sum of the digits in the even positions is a multiple of 11, then the number is divisible by 11. The rule of 12 combines the rules of 3 and 4, stating that if a number is divisible by both 3 and 4, it is divisible by 12.

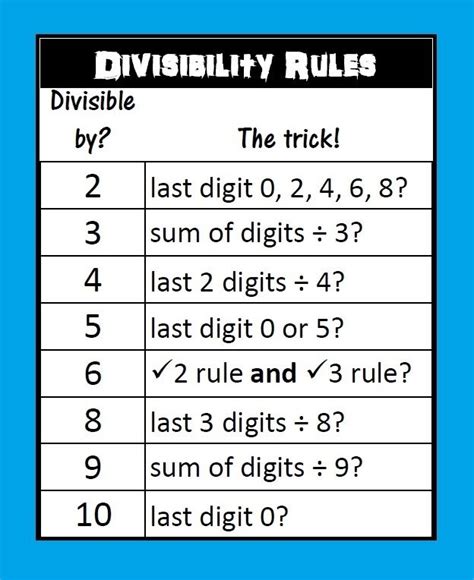
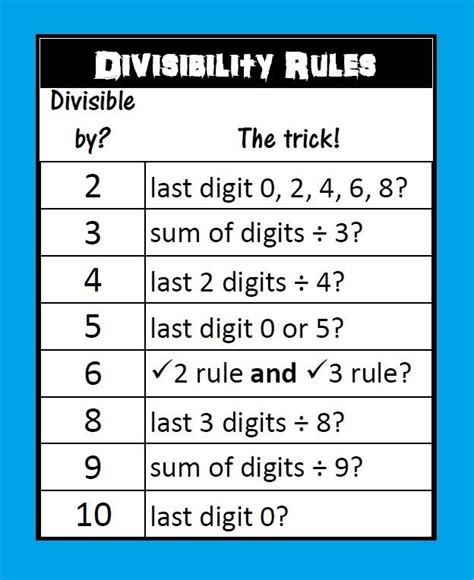
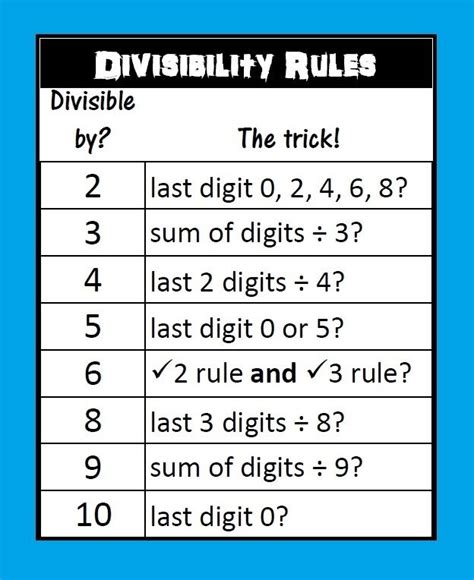
Divisibility Rules for 2, 3, 4, 5, 6, 7, 8, 9, and 10

The following are the divisibility rules for the numbers 2 through 10: * Rule of 2: If a number ends in 0, 2, 4, 6, or 8, it is divisible by 2. * Rule of 3: If the sum of the digits of a number is divisible by 3, then the number is divisible by 3. * Rule of 4: If the last two digits of a number form a number that is divisible by 4, then the original number is divisible by 4. * Rule of 5: If a number ends in 0 or 5, it is divisible by 5. * Rule of 6: If a number is divisible by both 2 and 3, it is divisible by 6. * Rule of 7: If the difference between twice the digit at the units place and the number formed by the remaining digits is divisible by 7, then the original number is divisible by 7. * Rule of 8: If the last three digits of a number form a number that is divisible by 8, then the original number is divisible by 8. * Rule of 9: If the sum of the digits of a number is divisible by 9, then the number is divisible by 9. * Rule of 10: If a number ends in 0, it is divisible by 10.

Benefits of Using Divisibility Rules

The benefits of using divisibility rules are numerous. They enable individuals to perform mathematical operations more efficiently, reducing the time and effort required to complete tasks. Additionally, divisibility rules help to improve mental math skills, allowing individuals to make calculations quickly and accurately. In educational settings, teaching divisibility rules can help students develop a deeper understanding of arithmetic and build a strong foundation for more advanced mathematical concepts.

Real-World Applications of Divisibility Rules

Divisibility rules have a wide range of real-world applications, including: * Science: Divisibility rules are used in scientific calculations, such as determining the number of molecules in a sample or calculating the volume of a substance. * Technology: Divisibility rules are used in computer programming and coding, where they are applied to algorithms and data analysis. * Engineering: Divisibility rules are used in engineering to design and optimize systems, such as bridges and buildings. * Finance: Divisibility rules are used in financial calculations, such as determining interest rates and investment returns.

Printable Divisibility Rules Sheet

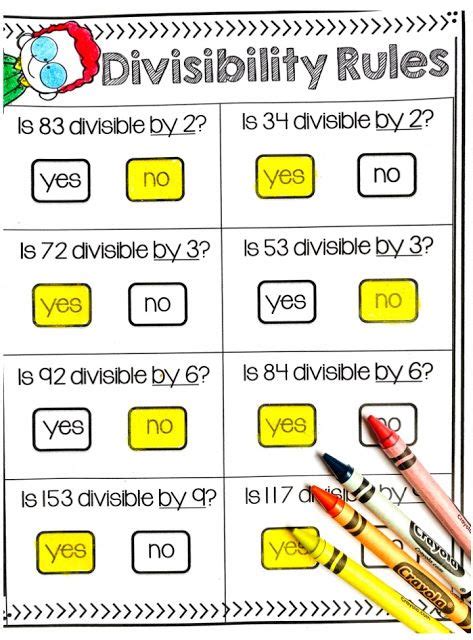
To help individuals learn and apply divisibility rules, a printable sheet can be a valuable resource. The sheet can include the basic divisibility rules, as well as rules for specific numbers. It can also provide examples and exercises to help individuals practice applying the rules. By using a printable divisibility rules sheet, individuals can improve their understanding of arithmetic and develop a strong foundation for more advanced mathematical concepts.

Tips for Using the Printable Divisibility Rules Sheet

The following are some tips for using the printable divisibility rules sheet: * Start by reviewing the basic divisibility rules and practicing applying them to simple numbers. * Gradually move on to more complex numbers and rules, such as the rule of 11 and the rule of 12. * Use the examples and exercises provided on the sheet to practice applying the rules and to test your understanding. * Keep the sheet handy and refer to it often, especially when working on mathematical problems or performing calculations.

Conclusion and Next Steps

In conclusion, divisibility rules are a fundamental concept in mathematics that can be applied to a wide range of real-world situations. By understanding and applying these rules, individuals can improve their mathematical skills, increase their efficiency, and make more informed decisions. To further develop your understanding of divisibility rules, it is recommended that you practice applying the rules to different numbers and scenarios. You can also explore more advanced mathematical concepts, such as prime numbers and modular arithmetic, to deepen your understanding of arithmetic and its applications.

Final Thoughts and Recommendations

In final thoughts, divisibility rules are a powerful tool that can be used to simplify mathematical operations and improve understanding of arithmetic. By using the printable divisibility rules sheet and practicing applying the rules, individuals can develop a strong foundation for more advanced mathematical concepts and improve their overall mathematical skills. It is recommended that you continue to practice and apply divisibility rules in different contexts to reinforce your understanding and develop your skills.

Divisibility Rules Image Gallery

What are divisibility rules?

+

Divisibility rules are a set of guidelines used to determine if a number can be divided evenly by another number.

Why are divisibility rules important?

+

Divisibility rules are important because they simplify mathematical operations, making them an indispensable tool in various fields, including science, technology, engineering, and mathematics (STEM).

How can I practice applying divisibility rules?

+

You can practice applying divisibility rules by using a printable divisibility rules sheet, which includes examples and exercises to help you develop your skills.

What are some real-world applications of divisibility rules?

+

Divisibility rules have a wide range of real-world applications, including science, technology, engineering, finance, and everyday life, where they are used to simplify mathematical operations and make informed decisions.

How can I use the printable divisibility rules sheet?

+

You can use the printable divisibility rules sheet to practice applying the rules, review the basic divisibility rules, and develop a strong foundation for more advanced mathematical concepts.

We hope that this article has provided you with a comprehensive understanding of divisibility rules and their applications. We encourage you to share this article with others, whether it be students, educators, or professionals, who can benefit from learning about divisibility rules. Additionally, we invite you to comment below with any questions or feedback you may have, and to explore our other resources and articles on mathematical concepts and applications. By working together, we can promote a deeper understanding of mathematics and its importance in our daily lives.