Intro
Discover unusual Even Odd Tips to simplify math, including number patterns, parity rules, and arithmetic shortcuts for effortless calculations and problem-solving strategies.
The world of numbers is fascinating, and one of the most basic yet intriguing concepts is the distinction between even and odd numbers. Understanding the properties and behaviors of even and odd numbers can be crucial in various mathematical operations and real-life applications. In this article, we will delve into the realm of even and odd numbers, exploring their definitions, properties, and practical uses, along with providing five even odd tips that can enhance your mathematical prowess and problem-solving skills.
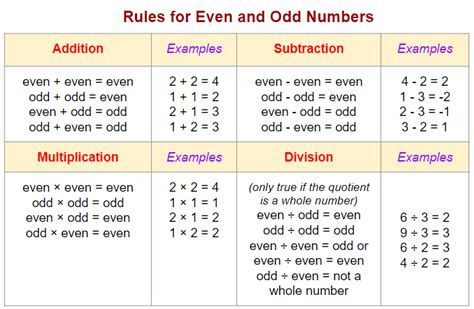
The distinction between even and odd numbers is fundamental. An even number is any integer that can be exactly divided by 2, such as 2, 4, 6, and so on. On the other hand, an odd number is any integer that cannot be exactly divided by 2, such as 1, 3, 5, and so on. This basic distinction has profound implications in mathematics and beyond. For instance, in physics, the parity of a particle (whether it behaves like an even or odd function under certain symmetry operations) is crucial for understanding its behavior and interactions.
Introduction to Even and Odd Numbers

The properties of even and odd numbers are essential for various mathematical operations. For example, the sum of two even numbers is always even, the sum of two odd numbers is always even, and the sum of an even and an odd number is always odd. Similarly, the product of two even numbers is always even, the product of two odd numbers is always odd, and the product of an even and an odd number is always even. Understanding these properties can simplify arithmetic operations and help in solving complex problems.
Properties of Even and Odd Numbers

Even and odd numbers also play a significant role in algebra and geometry. In algebra, the concept of even and odd functions is crucial. An even function satisfies the condition f(x) = f(-x) for all x in its domain, meaning it is symmetric with respect to the y-axis. An odd function satisfies the condition f(-x) = -f(x) for all x in its domain, meaning it shows rotational symmetry with respect to the origin. In geometry, the parity of a polygon's number of sides can influence its properties and the formulas used to calculate its area and perimeter.
Practical Applications of Even and Odd Numbers

Now, let's dive into the five even odd tips that can help you navigate the world of numbers more effectively:
- Identifying Patterns: Recognizing patterns in sequences of even and odd numbers can be incredibly useful. For instance, understanding that every other number in a sequence of natural numbers is even (or odd) can help in solving problems related to sequences and series.
- Simplifying Arithmetic: Knowing the properties of even and odd numbers can simplify arithmetic operations. For example, if you need to calculate the sum of several numbers and you know the parity (even or odd) of the sum of some of them, you can use the properties of even and odd numbers to deduce the parity of the total sum without calculating it explicitly.
- Understanding Parity in Algebra: In algebra, understanding whether a function is even or odd can significantly simplify the process of solving equations and graphing functions. For instance, knowing that a function is even tells you that its graph is symmetric with respect to the y-axis, which can help in sketching the graph.
- Applying to Real-Life Problems: Even and odd numbers appear in various real-life scenarios, such as in the structure of molecules, the arrangement of leaves on stems, and the patterns of animal coats. Recognizing and applying the principles of even and odd numbers can provide insights into these phenomena.
- Enhancing Problem-Solving Skills: Finally, practicing problems that involve even and odd numbers can enhance your problem-solving skills. It trains your mind to think logically and mathematically, which is beneficial not only in mathematics but also in other areas of life that require analytical thinking.
Enhancing Mathematical Skills with Even and Odd Numbers
In conclusion, the distinction between even and odd numbers is more than just a basic mathematical concept; it has profound implications and applications across various fields. By understanding the properties and behaviors of even and odd numbers and applying the five even odd tips provided, you can not only improve your mathematical skills but also develop a deeper appreciation for the intricate patterns and structures that underlie our world.
Gallery of Even and Odd Numbers
Even and Odd Numbers Image Gallery







What are even and odd numbers?
+Even numbers are integers that can be exactly divided by 2, while odd numbers are integers that cannot be exactly divided by 2.
What are the properties of even and odd numbers?
+The properties include the rules for addition and multiplication of even and odd numbers, such as the sum of two even numbers being even, the sum of two odd numbers being even, and the product of two even numbers being even.
How are even and odd numbers applied in real life?
+Even and odd numbers are applied in various real-life scenarios, including physics, chemistry, biology, and engineering, where understanding patterns and structures is crucial.
We hope this article has not only provided you with a deeper understanding of even and odd numbers but has also inspired you to explore the fascinating world of mathematics further. Whether you are a student looking to improve your mathematical skills or a professional seeking to apply mathematical concepts to real-world problems, the principles of even and odd numbers are sure to be of value. Feel free to share your thoughts, ask questions, or explore more topics related to mathematics and its applications.
