5 Ways Calculate Ratio

Calculating ratios is a fundamental skill in various fields, including mathematics, science, finance, and engineering. A ratio is a way of comparing two quantities by division, and it can be expressed as a fraction, decimal, or percentage. In this article, we will explore five ways to calculate ratios, providing you with a comprehensive understanding of the concept.

To begin with, ratios are used to describe the relationship between two quantities. For instance, if you have 3 apples and 4 oranges, the ratio of apples to oranges is 3:4. This can be expressed as a fraction (3/4), decimal (0.75), or percentage (75%). Understanding ratios is crucial in making informed decisions, solving problems, and analyzing data.

Ratios have numerous applications in real-life scenarios. In finance, ratios are used to evaluate a company's performance, such as the price-to-earnings ratio or the debt-to-equity ratio. In science, ratios are used to describe the composition of mixtures, such as the ratio of water to soil in a plant's growth medium. In engineering, ratios are used to design and optimize systems, such as the gear ratio in a mechanical system.

Introduction to Ratios

Before we dive into the five ways to calculate ratios, let's define what a ratio is. A ratio is a comparison of two numbers by division. It can be expressed as a fraction, decimal, or percentage. For example, if you have 2 boys and 3 girls in a class, the ratio of boys to girls is 2:3 or 2/3.

Types of Ratios

There are several types of ratios, including: * Part-to-part ratio: compares two parts of a whole * Part-to-whole ratio: compares a part to the whole * Rate ratio: compares two rates or speeds * Equivalent ratio: compares two equal ratios

Method 1: Using Fractions

The first method to calculate a ratio is by using fractions. To do this, simply divide the first quantity by the second quantity. For example, if you want to calculate the ratio of 6 boys to 8 girls, you can write it as a fraction: 6/8. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2. Therefore, the simplified ratio is 3/4.

Example: Calculating a Ratio Using Fractions

Suppose you want to calculate the ratio of 12 employees to 16 managers. To do this, you can write it as a fraction: 12/16. Simplifying this fraction by dividing both the numerator and the denominator by their GCD (4), you get 3/4.

Method 2: Using Decimals

The second method to calculate a ratio is by using decimals. To do this, simply divide the first quantity by the second quantity. For example, if you want to calculate the ratio of 6 boys to 8 girls, you can divide 6 by 8, which gives you 0.75.

Example: Calculating a Ratio Using Decimals

Suppose you want to calculate the ratio of 12 employees to 16 managers. To do this, you can divide 12 by 16, which gives you 0.75.

Method 3: Using Percentages

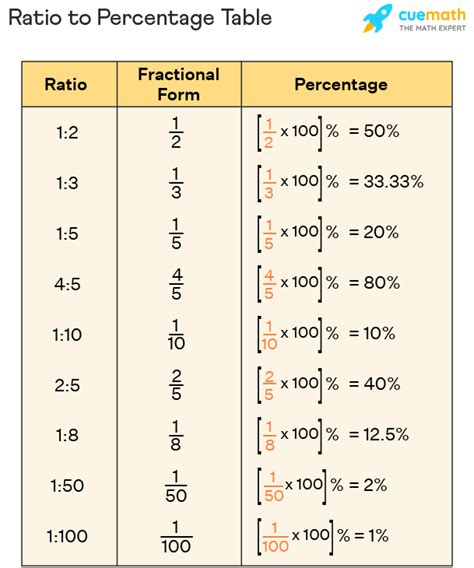
The third method to calculate a ratio is by using percentages. To do this, simply divide the first quantity by the second quantity and multiply by 100. For example, if you want to calculate the ratio of 6 boys to 8 girls, you can divide 6 by 8 and multiply by 100, which gives you 75%.

Example: Calculating a Ratio Using Percentages

Suppose you want to calculate the ratio of 12 employees to 16 managers. To do this, you can divide 12 by 16 and multiply by 100, which gives you 75%.

Method 4: Using Proportions

The fourth method to calculate a ratio is by using proportions. A proportion is a statement that two ratios are equal. For example, if you want to calculate the ratio of 6 boys to 8 girls, you can set up a proportion: 6/8 = x/10, where x is the unknown quantity.

Example: Calculating a Ratio Using Proportions

Suppose you want to calculate the ratio of 12 employees to 16 managers. To do this, you can set up a proportion: 12/16 = x/20, where x is the unknown quantity. Solving for x, you get x = 15.

Method 5: Using Equivalent Ratios

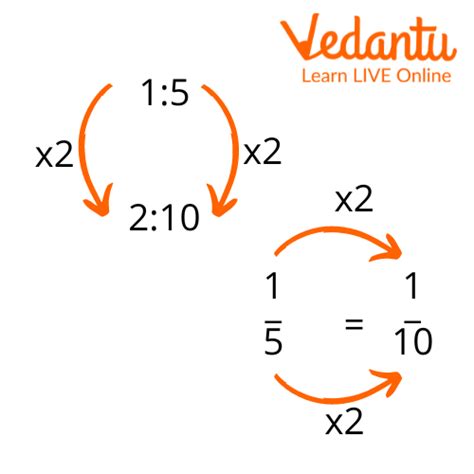
The fifth method to calculate a ratio is by using equivalent ratios. Equivalent ratios are ratios that have the same value. For example, if you want to calculate the ratio of 6 boys to 8 girls, you can find an equivalent ratio by multiplying or dividing both quantities by the same number. For instance, you can multiply both quantities by 2 to get 12/16, which is an equivalent ratio.

Example: Calculating a Ratio Using Equivalent Ratios

Suppose you want to calculate the ratio of 12 employees to 16 managers. To do this, you can find an equivalent ratio by multiplying or dividing both quantities by the same number. For instance, you can multiply both quantities by 3 to get 36/48, which is an equivalent ratio.

Ratio Calculation Image Gallery

What is a ratio?

+

A ratio is a comparison of two numbers by division. It can be expressed as a fraction, decimal, or percentage.

How do you calculate a ratio using fractions?

+

To calculate a ratio using fractions, simply divide the first quantity by the second quantity and simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD).

What are equivalent ratios?

+

Equivalent ratios are ratios that have the same value. They can be obtained by multiplying or dividing both quantities by the same number.

In conclusion, calculating ratios is an essential skill in various fields, and there are five methods to do so: using fractions, decimals, percentages, proportions, and equivalent ratios. By understanding these methods, you can effectively calculate and interpret ratios, making informed decisions and solving problems. We hope this article has provided you with a comprehensive understanding of ratio calculation and its applications. If you have any further questions or would like to share your thoughts, please comment below or share this article with your friends and colleagues.