5 Fraction To Decimal Conversions

Fraction to decimal conversions are a fundamental concept in mathematics, and understanding how to convert fractions to decimals is essential for various mathematical operations. In this article, we will delve into the world of fractions and decimals, exploring the importance of converting fractions to decimals and providing a comprehensive guide on how to perform these conversions.

Fractions and decimals are two different ways of representing numbers, and both have their own unique characteristics. Fractions are used to represent a part of a whole, while decimals are used to represent a number in terms of its place value. Converting fractions to decimals is a crucial step in many mathematical operations, such as addition, subtraction, multiplication, and division. It is also essential in real-world applications, such as science, engineering, and finance.

Converting fractions to decimals can be a straightforward process, but it requires a good understanding of the underlying concepts. In this article, we will explore the different methods of converting fractions to decimals, including the use of equivalent ratios, division, and conversion charts. We will also provide examples and practice problems to help illustrate the concepts and make them more accessible to readers.

Understanding Fractions and Decimals

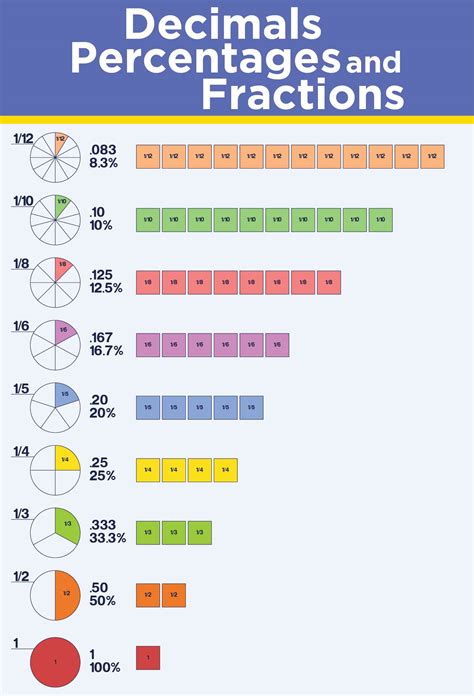
Before we dive into the world of fraction to decimal conversions, it is essential to understand the basics of fractions and decimals. A fraction is a way of representing a part of a whole, and it consists of a numerator and a denominator. The numerator represents the number of equal parts, while the denominator represents the total number of parts. For example, the fraction 3/4 represents three equal parts out of a total of four parts.

Decimals, on the other hand, are used to represent a number in terms of its place value. A decimal number consists of a whole number part and a fractional part, separated by a decimal point. For example, the decimal number 3.75 represents three whole units and seventy-five hundredths.

Methods of Converting Fractions to Decimals

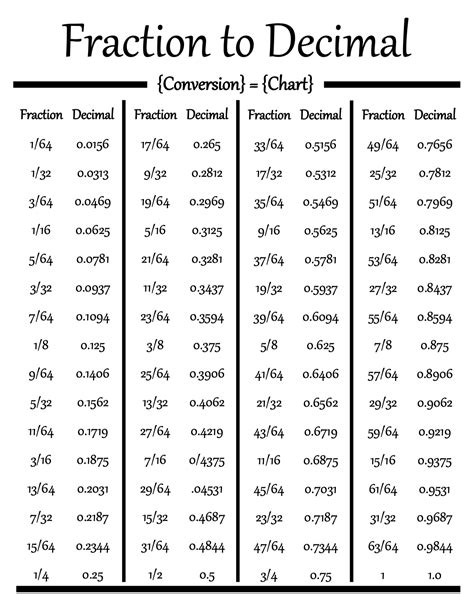
There are several methods of converting fractions to decimals, including the use of equivalent ratios, division, and conversion charts. The method you choose will depend on the complexity of the fraction and your personal preference.

One of the simplest methods of converting fractions to decimals is to use equivalent ratios. This involves finding an equivalent fraction with a denominator that is a power of 10. For example, to convert the fraction 3/4 to a decimal, you can find an equivalent fraction with a denominator of 10, such as 7.5/10. This fraction can then be converted to a decimal by dividing the numerator by the denominator.

Another method of converting fractions to decimals is to use division. This involves dividing the numerator by the denominator to get the decimal equivalent. For example, to convert the fraction 3/4 to a decimal, you can divide 3 by 4 to get 0.75.

Using Equivalent Ratios

Using equivalent ratios is a simple and effective way of converting fractions to decimals. To use this method, you need to find an equivalent fraction with a denominator that is a power of 10. For example, to convert the fraction 3/4 to a decimal, you can find an equivalent fraction with a denominator of 10, such as 7.5/10.

Here are the steps to follow:

• Find an equivalent fraction with a denominator that is a power of 10.
• Divide the numerator by the denominator to get the decimal equivalent.

For example, to convert the fraction 3/4 to a decimal using equivalent ratios, you can follow these steps:

• Find an equivalent fraction with a denominator of 10: 7.5/10
• Divide the numerator by the denominator: 7.5 ÷ 10 = 0.75

Using Division

Using division is another method of converting fractions to decimals. To use this method, you need to divide the numerator by the denominator to get the decimal equivalent.

Here are the steps to follow:

• Divide the numerator by the denominator to get the decimal equivalent.

For example, to convert the fraction 3/4 to a decimal using division, you can follow these steps:

• Divide the numerator by the denominator: 3 ÷ 4 = 0.75

Practice Problems

Now that we have explored the different methods of converting fractions to decimals, it's time to practice. Here are some practice problems to help you master the concepts:

• Convert the fraction 1/2 to a decimal using equivalent ratios.
• Convert the fraction 3/4 to a decimal using division.
• Convert the fraction 2/5 to a decimal using equivalent ratios.

Solutions:

• 1/2 = 0.5
• 3/4 = 0.75
• 2/5 = 0.4

Real-World Applications

Converting fractions to decimals is not just a mathematical concept; it has many real-world applications. In science, fractions are used to represent measurements, and converting them to decimals is essential for calculations. In engineering, fractions are used to represent ratios and proportions, and converting them to decimals is crucial for design and construction.

In finance, fractions are used to represent interest rates and investment returns, and converting them to decimals is essential for calculations. In everyday life, fractions are used to represent measurements, such as cooking recipes and building designs, and converting them to decimals is necessary for accurate calculations.

Science and Engineering

In science and engineering, fractions are used to represent measurements and ratios. Converting these fractions to decimals is essential for calculations and design.

For example, in chemistry, fractions are used to represent the concentration of solutions. Converting these fractions to decimals is necessary for calculations, such as determining the amount of solute needed to make a solution.

In engineering, fractions are used to represent ratios and proportions. Converting these fractions to decimals is crucial for design and construction, such as determining the stress on a beam or the load on a bridge.

Finance and Economics

In finance and economics, fractions are used to represent interest rates and investment returns. Converting these fractions to decimals is essential for calculations, such as determining the return on investment or the interest rate on a loan.

For example, in finance, fractions are used to represent interest rates, such as 3/4% or 1/2%. Converting these fractions to decimals is necessary for calculations, such as determining the interest rate on a loan or the return on investment.

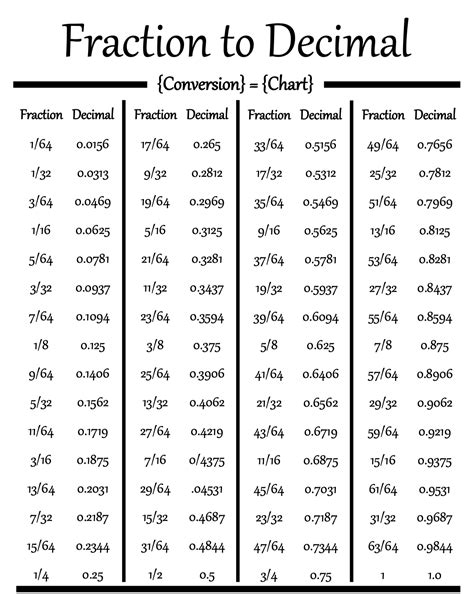
Gallery of Fraction to Decimal Conversions

Fraction to Decimal Conversions Image Gallery

Frequently Asked Questions

What is the difference between a fraction and a decimal?

+

A fraction is a way of representing a part of a whole, while a decimal is a way of representing a number in terms of its place value.

How do I convert a fraction to a decimal?

+

You can convert a fraction to a decimal by using equivalent ratios, division, or conversion charts.

What are some real-world applications of fraction to decimal conversions?

+

Fraction to decimal conversions have many real-world applications, including science, engineering, finance, and everyday life.

In conclusion, converting fractions to decimals is an essential mathematical concept with many real-world applications. By understanding the different methods of converting fractions to decimals, including equivalent ratios, division, and conversion charts, you can master this concept and apply it to various areas of your life. Whether you are a student, a professional, or simply someone who wants to improve your mathematical skills, this article has provided you with a comprehensive guide to fraction to decimal conversions. We hope that you have found this article informative and helpful, and we encourage you to practice the concepts and apply them to your everyday life. If you have any questions or comments, please do not hesitate to reach out to us.