Intro
Discover 5 ways to calculate ratio with ease, including proportion, fraction, and percentage methods, and learn how to apply ratio calculation in math, statistics, and real-world problems.
Calculating ratios is a fundamental concept in mathematics and statistics, and it has numerous applications in various fields, including business, finance, and science. A ratio is a way of comparing two quantities by division, and it can be expressed as a fraction, decimal, or percentage. In this article, we will explore five ways to calculate ratios, along with examples and practical applications.
To begin with, understanding ratios is crucial in making informed decisions, identifying trends, and solving problems. Ratios help us compare different quantities, identify proportions, and make predictions. Whether you are a student, a business professional, or a researcher, calculating ratios is an essential skill that can benefit you in many ways.
Ratios are used in various aspects of life, from cooking and construction to finance and engineering. For instance, a recipe might require a certain ratio of ingredients, while a building's design might depend on specific ratios of dimensions. In finance, ratios are used to evaluate a company's performance, liquidity, and profitability.
With the importance of ratios in mind, let's dive into the five ways to calculate them. Each method has its unique application and benefit, and understanding these methods can help you become more proficient in calculating and interpreting ratios.
Introduction to Ratios

Before we explore the five ways to calculate ratios, it's essential to understand the basics of ratios. A ratio is a comparison of two numbers, often denoted as a fraction, decimal, or percentage. The concept of ratios is used to describe the relationship between two quantities, and it has numerous applications in various fields.
To calculate a ratio, you need to divide one quantity by another. For example, if you want to calculate the ratio of boys to girls in a class, you would divide the number of boys by the number of girls. The result can be expressed as a fraction, decimal, or percentage.
Method 1: Simple Ratio Calculation

The simplest way to calculate a ratio is by dividing one quantity by another. This method is useful when you have two quantities and want to compare them directly. For example, if you have 10 boys and 15 girls in a class, the ratio of boys to girls can be calculated as follows:
Ratio = Number of boys / Number of girls = 10 / 15 = 2/3
This means that for every 2 boys, there are 3 girls in the class.
Method 2: Using Equivalent Ratios
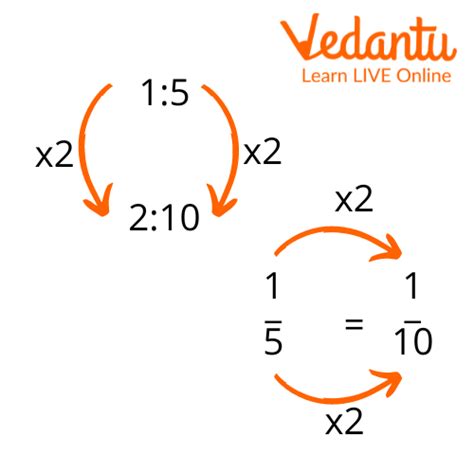
Equivalent ratios are ratios that have the same value but different quantities. This method is useful when you want to compare ratios that have different units or scales. For example, if you want to compare the ratio of boys to girls in two different classes, you can use equivalent ratios.
Let's say Class A has 10 boys and 15 girls, while Class B has 20 boys and 30 girls. To compare the ratios, you can simplify them to their simplest form:
Class A: 10/15 = 2/3 Class B: 20/30 = 2/3
Both classes have the same ratio of boys to girls, which is 2:3.
Method 3: Using Proportional Relationships
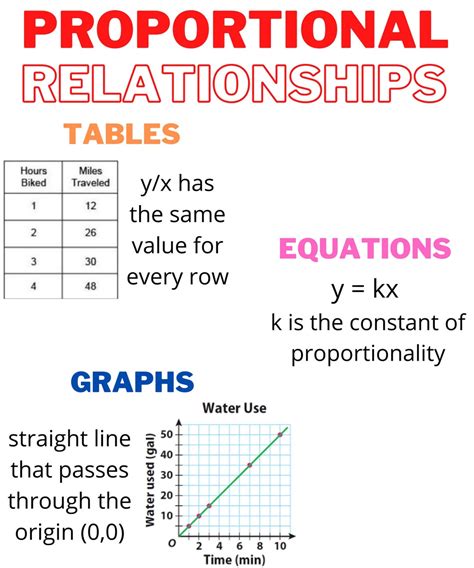
Proportional relationships are relationships between quantities that can be represented by a constant ratio. This method is useful when you want to identify patterns or trends in data. For example, if you want to analyze the relationship between the number of hours worked and the amount of money earned, you can use proportional relationships.
Let's say you earn $10 for every hour you work. If you work for 5 hours, you earn $50. If you work for 10 hours, you earn $100. The ratio of hours worked to money earned is constant, which is 1:10.
Method 4: Using Graphical Representations
Graphical representations are visual displays of data that can help you identify patterns and trends. This method is useful when you want to compare multiple ratios or identify relationships between different quantities. For example, if you want to analyze the relationship between the number of boys and girls in different classes, you can use a bar graph or a pie chart.
Let's say you have three classes with different numbers of boys and girls. You can create a bar graph to compare the ratios of boys to girls in each class. The graph can help you identify which class has the highest or lowest ratio of boys to girls.
Method 5: Using Algebraic Expressions

Algebraic expressions are mathematical expressions that use variables and constants to represent relationships between quantities. This method is useful when you want to solve problems that involve ratios and variables. For example, if you want to solve a problem that involves finding the ratio of two quantities when one of the quantities is unknown, you can use algebraic expressions.
Let's say you want to find the ratio of boys to girls in a class when the number of boys is unknown. You can use an algebraic expression to represent the ratio and solve for the unknown quantity.
Gallery of Ratio Calculations
Ratio Calculation Image Gallery










What is a ratio in mathematics?
+A ratio is a comparison of two numbers, often denoted as a fraction, decimal, or percentage.
How do you calculate a ratio?
+To calculate a ratio, you need to divide one quantity by another.
What are the five ways to calculate ratios?
+The five ways to calculate ratios are: simple ratio calculation, using equivalent ratios, using proportional relationships, using graphical representations, and using algebraic expressions.
In conclusion, calculating ratios is a fundamental concept in mathematics and statistics, and it has numerous applications in various fields. The five ways to calculate ratios, including simple ratio calculation, using equivalent ratios, using proportional relationships, using graphical representations, and using algebraic expressions, can help you become more proficient in calculating and interpreting ratios. By understanding these methods, you can make informed decisions, identify trends, and solve problems in various aspects of life. We invite you to share your thoughts, ask questions, or provide examples of how you have used ratios in your own life. Your feedback and engagement are valuable to us, and we look forward to hearing from you.
