5 Z Score Table Tips

Understanding the Z score table is crucial in statistics, particularly when dealing with normal distributions. The Z score, also known as a standard score, indicates how many standard deviations an element is from the mean. A Z score can be calculated using the formula Z = (X - μ) / σ, where X is the value of the element, μ is the mean of the dataset, and σ is the standard deviation. Here are a few opening paragraphs to introduce the topic and its importance.

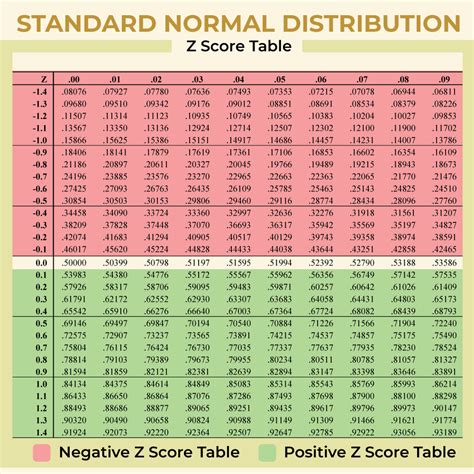
The Z score table, often referred to as the standard normal distribution table (Z-table), is a mathematical table that provides the probability that a random variable with a standard normal distribution will be less than or equal to a given Z score. This table is indispensable for hypothesis testing and confidence intervals, allowing researchers to determine the significance of their findings by comparing them against the standard normal distribution. The Z score table is structured in a way that the rows represent the Z score up to the first decimal place, and the columns represent the second decimal place.

The importance of understanding and effectively using the Z score table cannot be overstated. It is a fundamental tool in statistical analysis, enabling the calculation of probabilities and the interpretation of data in various fields such as medicine, social sciences, and engineering. For instance, in quality control, manufacturers might use Z scores to identify which products are significantly different from the mean in terms of quality, helping to maintain high standards. Similarly, in finance, Z scores can be used to predict the likelihood of a company going bankrupt based on a combination of financial metrics.

In educational settings, students often struggle with interpreting Z scores and using the Z score table due to its complexity and the abstract nature of statistical concepts. However, mastering the Z score table is essential for progressing in fields that rely heavily on statistical analysis. It allows for the comparison of data points within a normal distribution, facilitating the identification of outliers, the calculation of probabilities, and the making of informed decisions based on data.

Introduction to Z Score Table

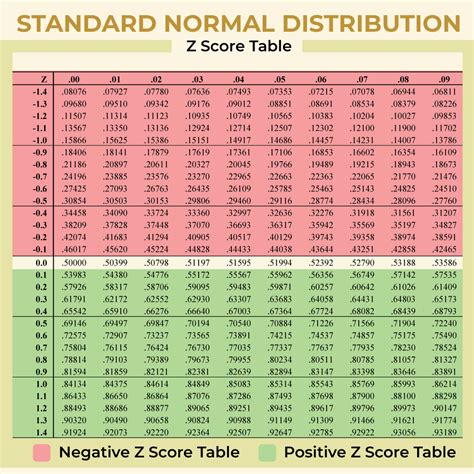
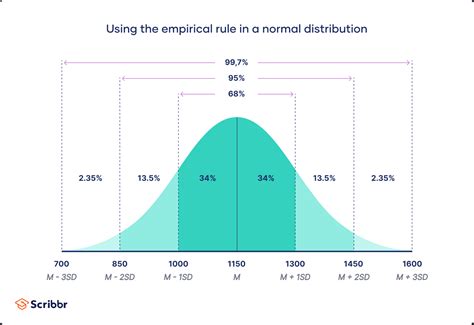
The Z score table is a comprehensive tool that lists the area under the standard normal curve to the left of a given Z score. This area represents the probability that a random variable with a standard normal distribution will have a value less than or equal to the given Z score. The table is typically arranged with Z scores ranging from -3.09 to 3.09, covering the vast majority of the distribution, given that about 99.8% of the values lie within three standard deviations of the mean in a normal distribution.

Understanding Z Score Calculation

To calculate a Z score, one needs the value of the element (X), the mean of the dataset (μ), and the standard deviation (σ) of the dataset. The formula Z = (X - μ) / σ calculates how many standard deviations away from the mean our value is. A positive Z score indicates that the value is above the mean, while a negative Z score indicates that it is below the mean. For example, a Z score of 2 means that the value is 2 standard deviations above the mean.

Interpreting the Z Score Table

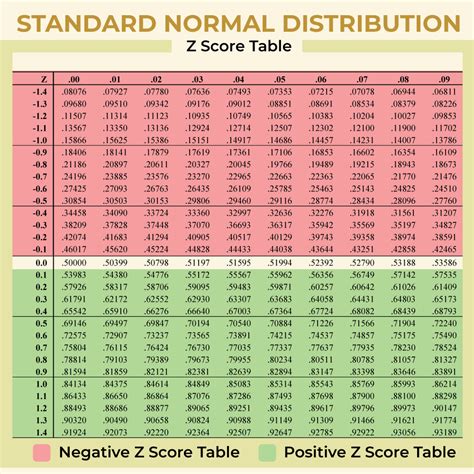
Interpreting the Z score table involves finding the probability that a value is less than or equal to a given Z score. The table provides the area to the left of the Z score, which directly corresponds to this probability. For instance, if the Z score is 1.5, one would look up 1.5 in the Z score table to find the probability that a random variable is less than or equal to 1.5 standard deviations above the mean.

Practical Applications of Z Scores

Z scores have numerous practical applications across various fields:

Quality Control: Identifying products that are significantly different from the average quality.
Finance: Predicting bankruptcy through financial metrics.
Medicine: Determining the likelihood of a patient having a certain condition based on test results.
Education: Identifying students who are significantly above or below the average performance.

Tips for Using the Z Score Table

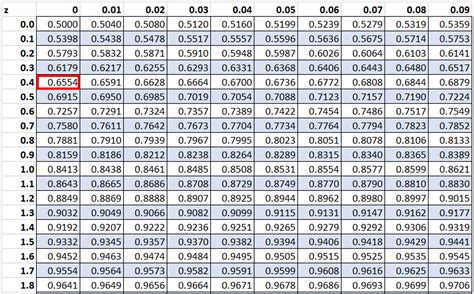
Here are some tips for effectively using the Z score table:

Understand the Z Score Formula: Before using the table, ensure you understand how to calculate a Z score.
Identify the Correct Z Score: Make sure to look up the correct Z score in the table, considering both the first and second decimal places.
Interpret the Results Correctly: Remember that the table gives the area to the left of the Z score, which is the probability that a value is less than or equal to the given Z score.
Consider the Direction of the Z Score: Positive Z scores indicate values above the mean, while negative Z scores indicate values below the mean.
Practice with Examples: The more you practice using the Z score table with different examples, the more comfortable you will become with interpreting Z scores and applying them in real-world scenarios.

Common Mistakes to Avoid

When working with Z scores and the Z score table, it's essential to avoid common mistakes such as:

Incorrectly calculating the Z score due to misunderstanding the formula.
Looking up the wrong Z score in the table.
Misinterpreting the probability given by the table.
Not considering the direction of the Z score (positive or negative).

Conclusion and Future Directions

In conclusion, mastering the use of the Z score table is a fundamental skill for anyone involved in statistical analysis. By understanding how to calculate Z scores, interpret the Z score table, and apply this knowledge in practical scenarios, individuals can make more informed decisions based on data. As data analysis continues to play an increasingly critical role in various fields, the importance of Z scores and the Z score table will only continue to grow.

Z Score Table Image Gallery

What is a Z score in statistics?

A Z score, or standard score, is a measure of how many standard deviations an element is from the mean. It is calculated using the formula Z = (X - μ) / σ, where X is the value of the element, μ is the mean of the dataset, and σ is the standard deviation.

How do I interpret the Z score table?

The Z score table provides the area under the standard normal curve to the left of a given Z score, which represents the probability that a random variable with a standard normal distribution will have a value less than or equal to the given Z score.

What are some common applications of Z scores?

Z scores have applications in quality control, finance, medicine, and education, among other fields. They are used for predicting outcomes, identifying outliers, and making informed decisions based on statistical analysis.

How do I calculate a Z score?

To calculate a Z score, use the formula Z = (X - μ) / σ, where X is the value of the element, μ is the mean of the dataset, and σ is the standard deviation.

Why is understanding the Z score table important?

Understanding the Z score table is crucial for statistical analysis, hypothesis testing, and confidence intervals. It helps in determining the significance of findings and making informed decisions based on data.

We hope this comprehensive guide to the Z score table has been informative and helpful. Whether you're a student, researcher, or professional, mastering the Z score table can significantly enhance your ability to analyze and interpret data. Feel free to share your thoughts, ask questions, or seek further clarification on any of the topics discussed. Your engagement and feedback are invaluable in helping us provide the best possible content and support for your statistical analysis needs.