5 Coordinate Plane Graph Tips

Understanding the coordinate plane is a fundamental concept in mathematics, particularly in algebra and geometry. It provides a visual representation of mathematical relationships, allowing individuals to graph points, lines, and other geometric shapes. Mastering the coordinate plane is essential for problem-solving and critical thinking in various fields, including science, engineering, and economics. In this article, we will delve into the world of coordinate plane graphs, exploring their importance, and providing valuable tips for working with them effectively.

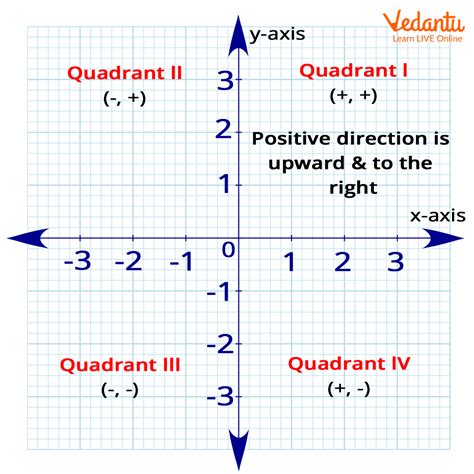
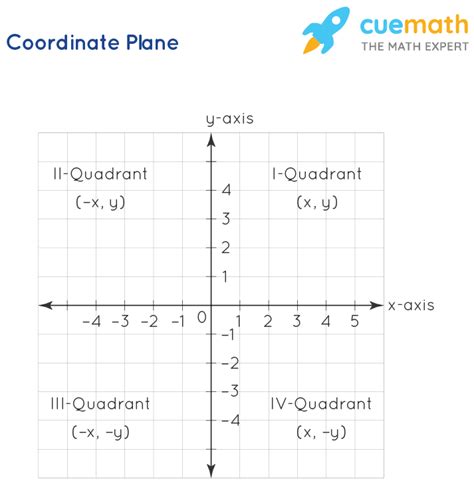
The coordinate plane, also known as the Cartesian plane, is a two-dimensional plane with an x-axis and a y-axis. The x-axis represents the horizontal direction, while the y-axis represents the vertical direction. The point where the two axes intersect is called the origin, denoted as (0, 0). Each point on the plane is represented by a pair of coordinates (x, y), which indicate its position relative to the origin. The coordinate plane is divided into four quadrants: I, II, III, and IV, depending on the signs of the x and y coordinates.

To fully appreciate the power of coordinate plane graphs, it is crucial to understand their applications in real-world scenarios. From mapping the trajectory of projectiles to analyzing the growth of populations, coordinate plane graphs offer a versatile tool for visualizing and interpreting complex data. By recognizing the significance of these graphs, individuals can unlock new insights and develop a deeper understanding of the world around them.

Understanding Coordinate Plane Basics

Before diving into advanced graphing techniques, it is essential to grasp the fundamental concepts of the coordinate plane. This includes understanding the x and y axes, identifying quadrants, and plotting points. A solid foundation in these basics will enable individuals to tackle more complex graphing tasks with confidence.

Plotting Points and Lines

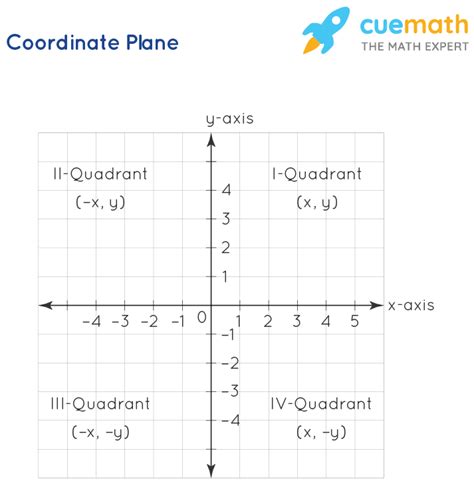
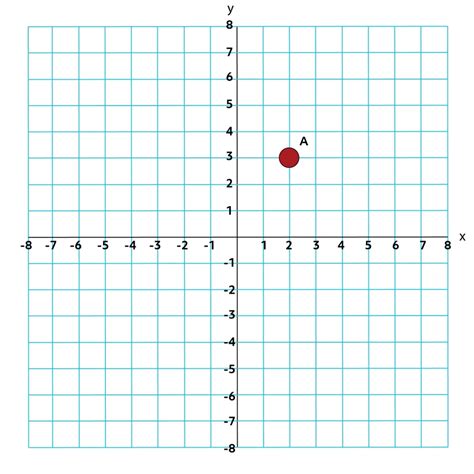
Plotting points and lines is a critical aspect of working with coordinate plane graphs. To plot a point, simply locate the x and y coordinates on the respective axes and mark the intersection. For lines, individuals can use the slope-intercept form (y = mx + b) or the point-slope form (y - y1 = m(x - x1)) to determine the equation of the line. By mastering these techniques, individuals can effectively visualize and analyze linear relationships.

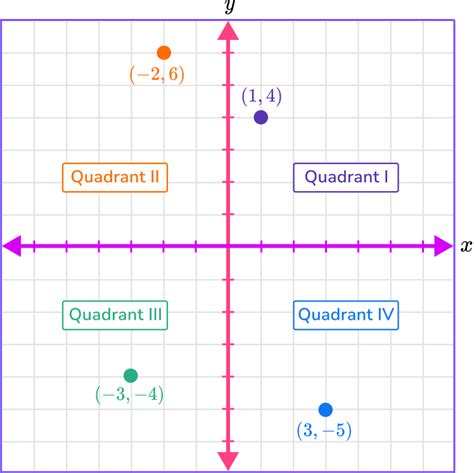
Working with Quadrants

The coordinate plane is divided into four quadrants, each with its unique characteristics. Quadrant I has positive x and y coordinates, Quadrant II has negative x and positive y coordinates, Quadrant III has negative x and y coordinates, and Quadrant IV has positive x and negative y coordinates. Understanding the properties of each quadrant is vital for graphing and analyzing functions, as well as solving problems involving trigonometry and geometry.

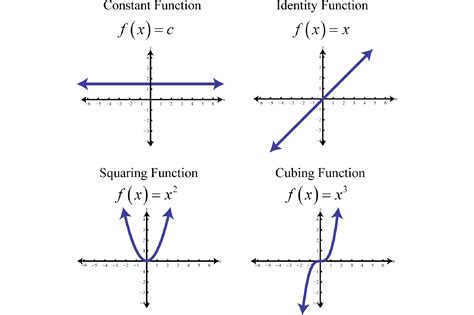
Graphing Functions

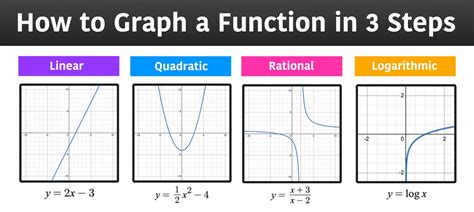
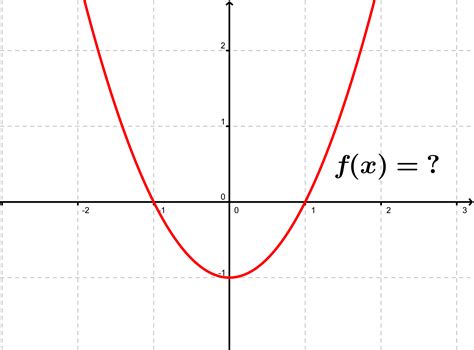
Graphing functions is a powerful tool for visualizing and analyzing mathematical relationships. By plotting points and connecting them with lines or curves, individuals can identify patterns, trends, and correlations. Common types of functions include linear, quadratic, polynomial, and rational functions, each with its unique graphing characteristics. Mastering function graphing enables individuals to model real-world phenomena, make predictions, and solve complex problems.

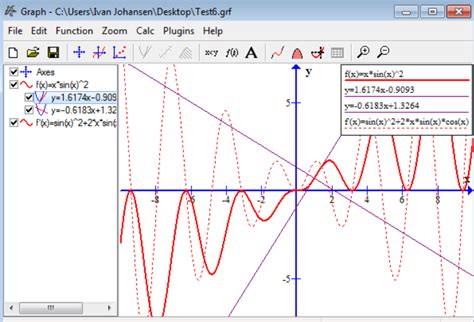
Using Graphing Tools and Software

In today's digital age, graphing tools and software have become indispensable for working with coordinate plane graphs. From graphing calculators to computer algebra systems, these tools offer a range of features and functionalities that can simplify and enhance the graphing process. By familiarizing themselves with these tools, individuals can streamline their workflow, explore complex graphs, and develop a deeper understanding of mathematical concepts.

Coordinate Plane Graph Tips

Here are five valuable tips for working with coordinate plane graphs: * Always label the x and y axes, and include a title for the graph. * Use a consistent scale for the x and y axes to ensure accurate representations. * Plot points carefully, using a ruler or other straightedge to ensure accuracy. * Use different colors or line styles to distinguish between multiple functions or graphs. * Take advantage of graphing tools and software to explore complex graphs and functions.

By following these tips and mastering the fundamentals of coordinate plane graphs, individuals can unlock new insights and develop a deeper understanding of mathematical relationships. Whether in academia, profession, or personal projects, the ability to work effectively with coordinate plane graphs is an invaluable skill that can open doors to new opportunities and discoveries.

Coordinate Plane Graph Image Gallery

What is the coordinate plane?

The coordinate plane, also known as the Cartesian plane, is a two-dimensional plane with an x-axis and a y-axis. It provides a visual representation of mathematical relationships, allowing individuals to graph points, lines, and other geometric shapes.

How do I plot a point on the coordinate plane?

To plot a point, simply locate the x and y coordinates on the respective axes and mark the intersection. For example, to plot the point (3, 4), locate the x-coordinate (3) on the x-axis and the y-coordinate (4) on the y-axis, and mark the intersection.

What are the different types of functions that can be graphed on the coordinate plane?

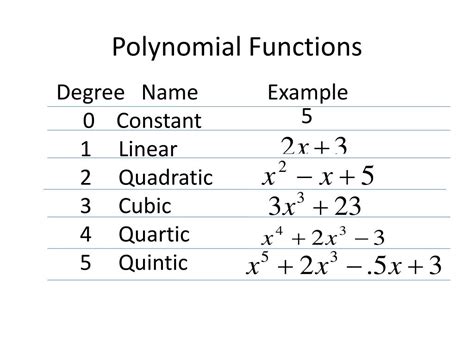
Common types of functions that can be graphed on the coordinate plane include linear, quadratic, polynomial, and rational functions. Each type of function has its unique graphing characteristics, and understanding these characteristics is essential for visualizing and analyzing mathematical relationships.

How can I use graphing tools and software to enhance my understanding of coordinate plane graphs?

Graphing tools and software, such as graphing calculators and computer algebra systems, offer a range of features and functionalities that can simplify and enhance the graphing process. By familiarizing yourself with these tools, you can streamline your workflow, explore complex graphs, and develop a deeper understanding of mathematical concepts.

What are some real-world applications of coordinate plane graphs?

Coordinate plane graphs have numerous real-world applications, including mapping the trajectory of projectiles, analyzing the growth of populations, and modeling complex systems. By recognizing the significance of these graphs, individuals can unlock new insights and develop a deeper understanding of the world around them.

In summary, mastering the art of working with coordinate plane graphs is an essential skill for anyone interested in mathematics, science, or engineering. By understanding the basics of the coordinate plane, plotting points and lines, working with quadrants, graphing functions, and using graphing tools and software, individuals can unlock new insights and develop a deeper understanding of mathematical relationships. Whether you are a student, professional, or simply a curious learner, we encourage you to explore the world of coordinate plane graphs and discover the many wonders that it holds. Share your thoughts, ask questions, and join the conversation to further enhance your understanding of this fascinating topic.