5 Polar Graph Tips

Polar graphs are a unique and fascinating way to visualize data, offering a distinct perspective on the relationships between variables. Unlike Cartesian graphs, which use x and y axes, polar graphs utilize a radial distance from a central point and the angle from a reference direction, typically the positive x-axis. This makes them particularly useful for representing data that has directional or cyclic characteristics, such as wind directions, sound waves, or the orbits of celestial bodies. The importance of understanding and effectively using polar graphs cannot be overstated, as they provide insights that might be obscured in traditional Cartesian coordinates.

The versatility of polar graphs extends into various fields, including physics, engineering, and data analysis. For instance, in physics, polar graphs are instrumental in describing the motion of objects in circular paths or in representing complex numbers. In engineering, they are used for designing and analyzing systems that involve rotational motion or cyclic patterns. Furthermore, data analysts leverage polar graphs to visualize and understand patterns in data that have a cyclic or directional nature, such as time-series data or geographic information.

Understanding how to work with polar graphs is essential for anyone involved in these fields. It requires a good grasp of trigonometry and the ability to interpret data in a non-traditional coordinate system. However, with practice and the right tips, creating and interpreting polar graphs can become second nature. This article aims to provide a comprehensive guide to getting the most out of polar graphs, including tips on their creation, interpretation, and application.

Introduction to Polar Graphs

Polar graphs are plotted on a polar coordinate system, where each point is determined by a distance from a reference point (the origin) and the angle from a reference direction (usually the positive x-axis). This system is particularly useful for representing functions that have a periodic nature or for visualizing data that involves directions or angles, such as the velocity of wind or the trajectory of projectiles.

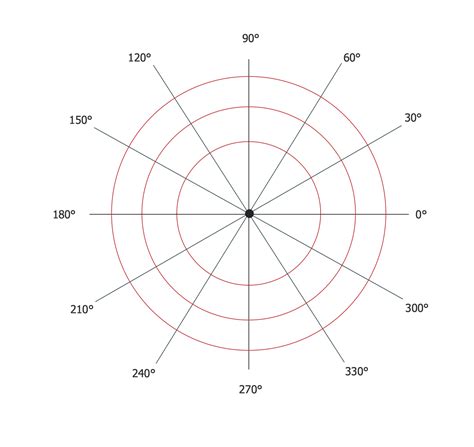
Key Components of Polar Graphs

To fully utilize polar graphs, it's essential to understand their key components: - **Polar Axis:** The reference line from which angles are measured, usually drawn horizontally and deemed the polar axis. - **Origin:** The central point from which distances are measured. - **Radius Vector:** A line segment that connects the origin to a point on the graph, representing the distance from the origin to that point. - **Angle:** Measured counterclockwise from the polar axis to the radius vector, it determines the direction of the point from the origin.

Creating Polar Graphs

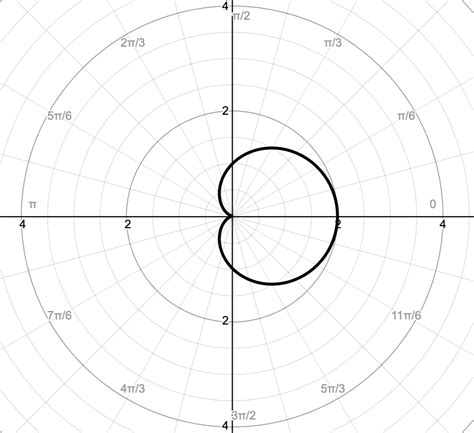
Creating a polar graph involves several steps, from understanding the function or data you want to plot to actually drawing the graph. Here are some tips for creating polar graphs: 1. **Understand Your Function:** Before plotting, ensure you understand the nature of the function. Is it periodic? Does it have any symmetries? 2. **Choose the Right Scale:** The scale of your graph can significantly affect its readability. Ensure that the radius and angle scales are appropriate for the data. 3. **Plot Key Points:** Identify and plot key points such as where the function intersects the polar axis or where it reaches its maximum and minimum values. 4. **Connect the Dots:** Finally, connect the plotted points to form the graph, taking care to represent the function accurately, especially where it may loop back on itself or exhibit other complex behaviors.

Common Challenges in Creating Polar Graphs

When creating polar graphs, several challenges may arise: - **Complex Functions:** Functions with multiple loops or sharp turns can be difficult to plot accurately. - **Scaling:** Finding the right scale to represent the data effectively without overcrowding the graph or losing important details. - **Interpretation:** Understanding what the graph represents, especially for those not familiar with polar coordinates.

Interpreting Polar Graphs

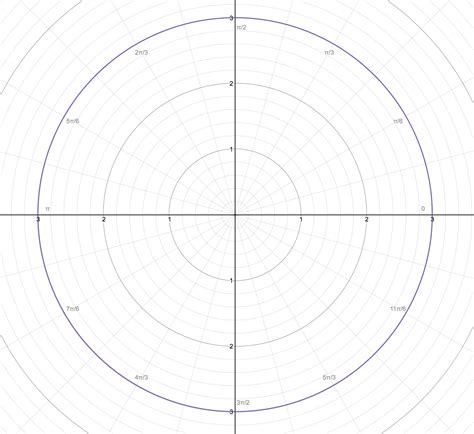
Interpreting polar graphs requires a good understanding of the polar coordinate system and the nature of the data being represented. Here are some tips for interpreting polar graphs: - **Look for Symmetry:** Polar graphs can exhibit several types of symmetry, including rotational symmetry and reflection symmetry. - **Identify Periodicity:** Many functions plotted in polar coordinates are periodic, meaning they repeat after a certain angle. - **Analyze Loops and Curves:** The shape of the graph can provide insights into the nature of the function or data, such as the presence of loops indicating periodic behavior.

Applications of Polar Graphs

Polar graphs have a wide range of applications: - **Physics and Engineering:** For describing circular motion, representing complex numbers, and analyzing systems with rotational symmetry. - **Data Analysis:** Especially useful for visualizing cyclic patterns in data, such as daily, monthly, or yearly trends. - **Navigation and Geography:** For representing directions and distances in a more intuitive manner than Cartesian coordinates.

Advanced Techniques in Polar Graphing

For those looking to advance their skills in polar graphing, several techniques can enhance the utility and appearance of polar graphs: - **Combining Functions:** Plotting multiple functions on the same graph can help compare their behaviors. - **Using Different Colors:** Color can be used to differentiate between functions, highlight specific features, or represent additional data dimensions. - **Interactive Graphs:** Creating interactive polar graphs allows for real-time exploration of how functions behave as parameters are changed.

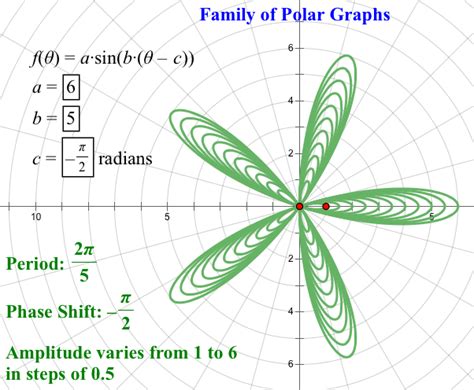
Tools for Creating Polar Graphs

Several tools are available for creating polar graphs, ranging from traditional graph paper to sophisticated computer software: - **Graphing Calculators:** Many graphing calculators have the capability to plot polar graphs, offering a portable and efficient way to explore functions. - **Computer Software:** Programs like MATLAB, Mathematica, and certain graphing apps can create complex polar graphs with ease, often including features for customization and analysis. - **Online Platforms:** There are also online tools and platforms that allow users to create and share polar graphs, which can be particularly useful for educational purposes or collaboration.

Polar Graph Image Gallery

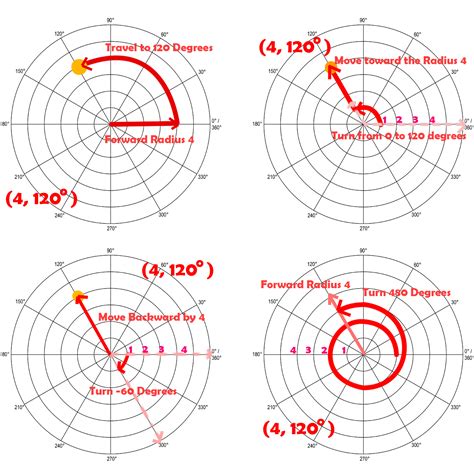
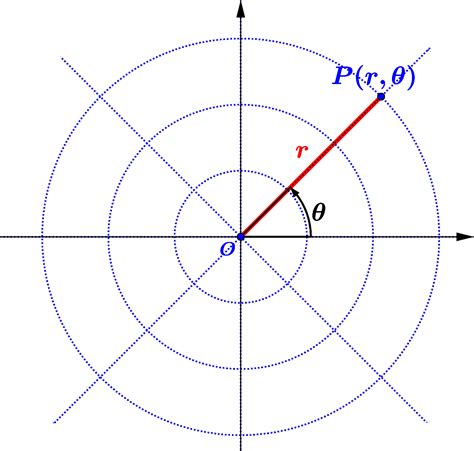
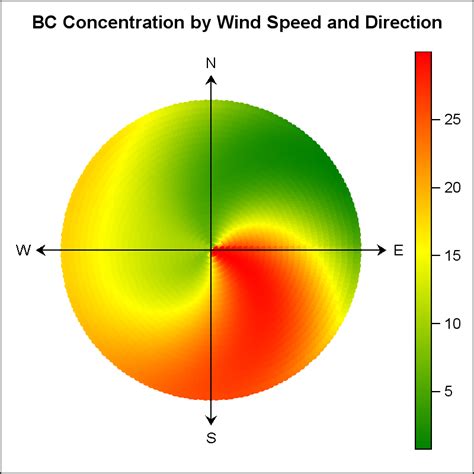
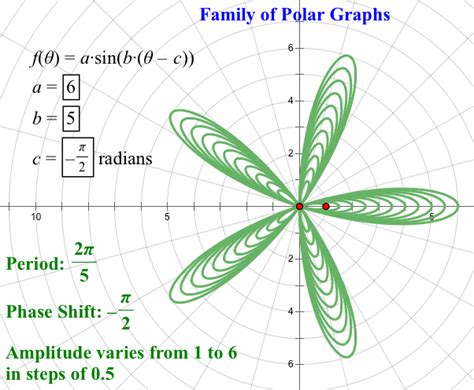
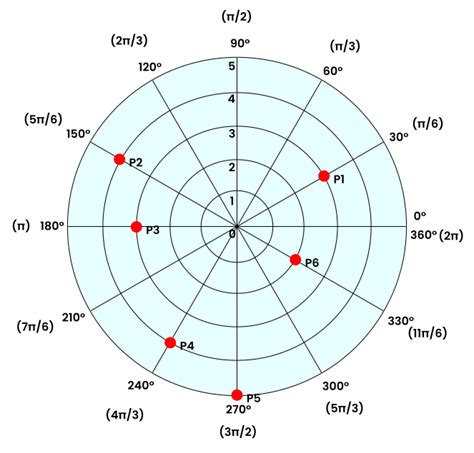
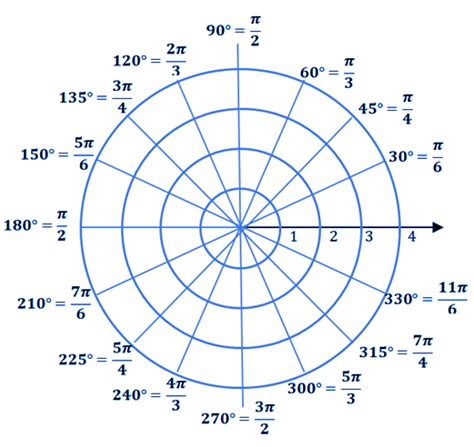
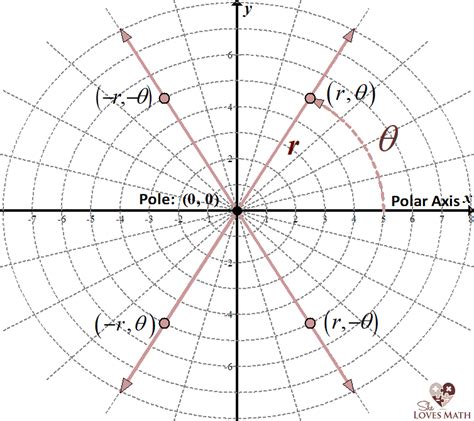
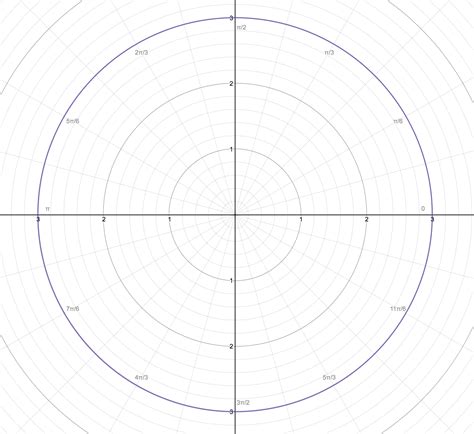
What are polar graphs used for?

Polar graphs are used for representing functions or data that have a cyclic or directional nature, such as wind patterns, sound waves, or the orbits of celestial bodies.

How do you create a polar graph?

To create a polar graph, you need to understand the function or data, choose the right scale, plot key points, and then connect these points to form the graph.

What are the advantages of using polar graphs?

Polar graphs offer a unique perspective on data, especially useful for visualizing cyclic patterns, directions, or periodic behaviors, making them invaluable in various scientific and engineering applications.

In conclusion, polar graphs are a powerful tool for visualizing and analyzing data with cyclic or directional characteristics. By understanding how to create, interpret, and apply polar graphs, individuals in various fields can gain deeper insights into their data and make more informed decisions. Whether you're a student looking to enhance your understanding of mathematics and physics or a professional seeking to leverage advanced data analysis techniques, mastering polar graphs can be a valuable skill. We invite you to share your experiences with polar graphs, ask questions, or explore further resources on this fascinating topic.