Intro
Discover the ultimate Unit Circle Chart Printable, featuring trigonometric functions, angles, and radians, perfect for math students and educators, with printable templates and charts for easy reference and learning.
The unit circle is a fundamental concept in mathematics, particularly in trigonometry and geometry. It is a circle with a radius of 1 unit, centered at the origin of a coordinate plane. The unit circle is used to define the trigonometric functions, such as sine, cosine, and tangent, and is essential for solving problems in various fields, including physics, engineering, and computer science. In this article, we will explore the importance of the unit circle, its properties, and how to use a unit circle chart printable to better understand this concept.
The unit circle is a powerful tool for visualizing and calculating trigonometric relationships. It is a circle with a radius of 1 unit, which means that the distance from the center of the circle to any point on the circle is 1 unit. The unit circle is typically centered at the origin (0, 0) of a coordinate plane, which allows us to use the x and y coordinates of points on the circle to define the trigonometric functions. The unit circle is also symmetric about the x and y axes, which makes it easier to work with.
The unit circle has several key properties that make it useful for solving trigonometric problems. One of the most important properties is the definition of the trigonometric functions. The sine, cosine, and tangent of an angle are defined as the ratios of the lengths of the sides of a right triangle formed by a point on the unit circle and the x and y axes. The sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse, the cosine is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse, and the tangent is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
Understanding the Unit Circle
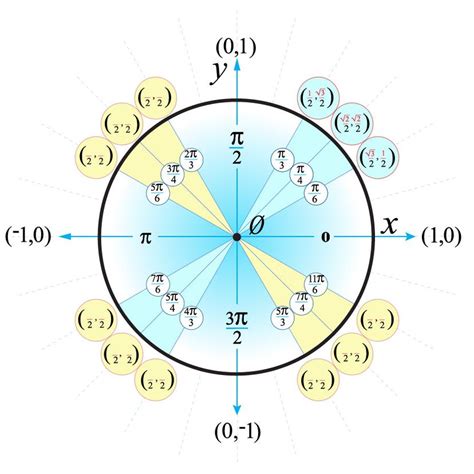
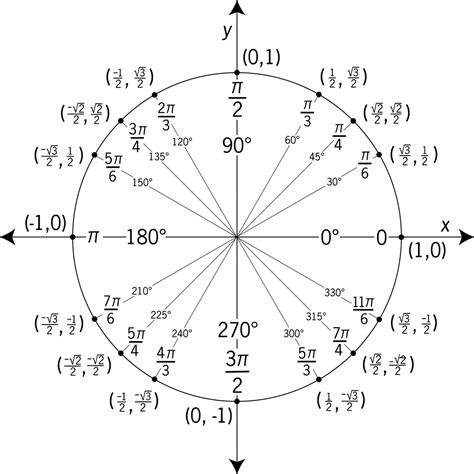
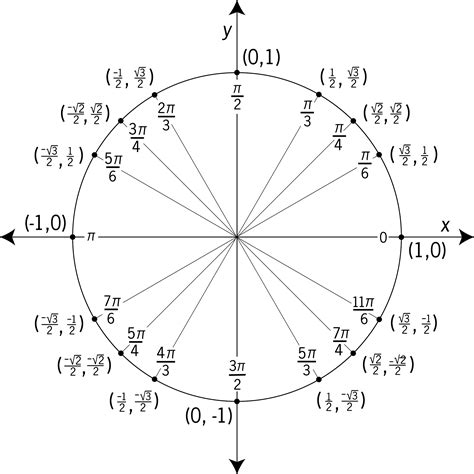
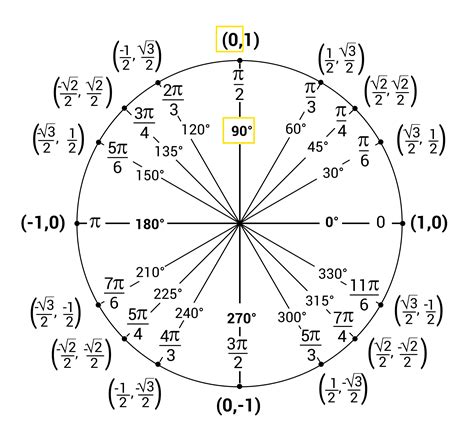
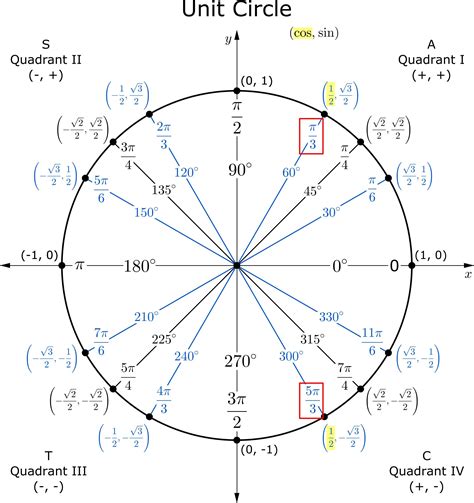
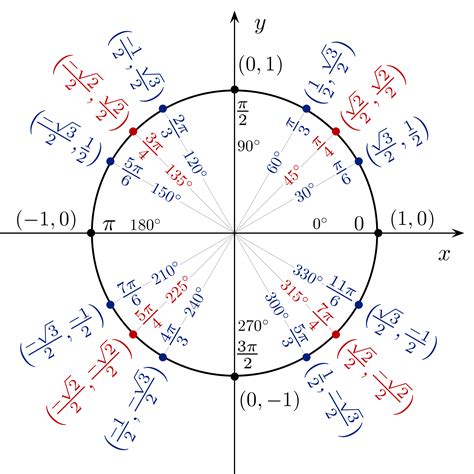
To better understand the unit circle, it is helpful to use a unit circle chart printable. A unit circle chart is a diagram that shows the unit circle with the x and y axes, as well as the trigonometric functions of common angles. The chart typically includes the sine, cosine, and tangent of angles from 0 to 360 degrees, as well as the corresponding x and y coordinates of points on the circle. Using a unit circle chart printable can help you to visualize the relationships between the trigonometric functions and to calculate the values of the functions for specific angles.
Properties of the Unit Circle
The unit circle has several key properties that make it useful for solving trigonometric problems. Some of the most important properties include: * The unit circle is symmetric about the x and y axes. * The unit circle has a radius of 1 unit. * The trigonometric functions are defined as the ratios of the lengths of the sides of a right triangle formed by a point on the unit circle and the x and y axes. * The sine, cosine, and tangent of an angle are periodic functions, with a period of 360 degrees.Using a Unit Circle Chart Printable
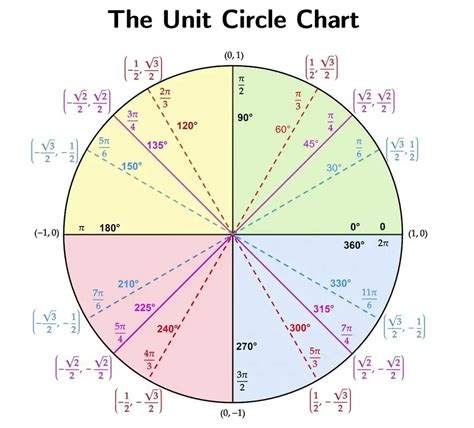
Using a unit circle chart printable can help you to visualize the relationships between the trigonometric functions and to calculate the values of the functions for specific angles. To use a unit circle chart, start by identifying the angle for which you want to calculate the trigonometric functions. Next, find the corresponding point on the unit circle and read off the x and y coordinates. Finally, use the x and y coordinates to calculate the sine, cosine, and tangent of the angle.
Benefits of Using a Unit Circle Chart
Using a unit circle chart printable has several benefits, including: * It can help you to visualize the relationships between the trigonometric functions. * It can help you to calculate the values of the trigonometric functions for specific angles. * It can help you to identify the periodic properties of the trigonometric functions. * It can help you to solve problems in various fields, including physics, engineering, and computer science.Creating a Unit Circle Chart Printable
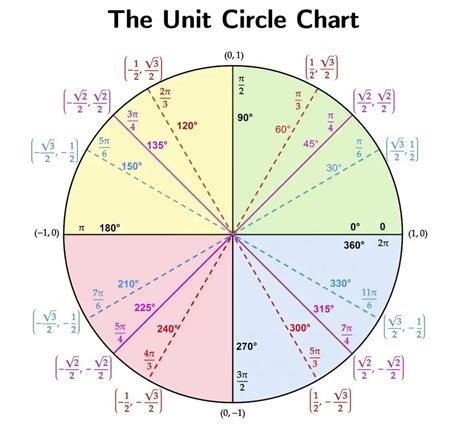
To create a unit circle chart printable, start by drawing a circle with a radius of 1 unit, centered at the origin of a coordinate plane. Next, draw the x and y axes and label the points on the circle where the axes intersect. Then, calculate the x and y coordinates of points on the circle for common angles, such as 30, 45, 60, and 90 degrees. Finally, use the x and y coordinates to calculate the sine, cosine, and tangent of the angles and create a chart that shows the values of the functions.
Tips for Creating a Unit Circle Chart
Here are some tips for creating a unit circle chart printable: * Use a graph paper to draw the circle and the x and y axes. * Label the points on the circle where the axes intersect. * Calculate the x and y coordinates of points on the circle for common angles. * Use the x and y coordinates to calculate the sine, cosine, and tangent of the angles. * Create a chart that shows the values of the functions for common angles.Applications of the Unit Circle

The unit circle has several applications in various fields, including physics, engineering, and computer science. Some of the most important applications include:
- Calculating the trajectories of projectiles.
- Modeling the motion of objects in circular orbits.
- Analyzing the vibrations of mechanical systems.
- Creating computer graphics and animations.
Real-World Examples of the Unit Circle
Here are some real-world examples of the unit circle: * The motion of a pendulum can be modeled using the unit circle. * The trajectory of a projectile can be calculated using the unit circle. * The vibrations of a mechanical system can be analyzed using the unit circle. * The motion of a car on a circular track can be modeled using the unit circle.Conclusion and Final Thoughts
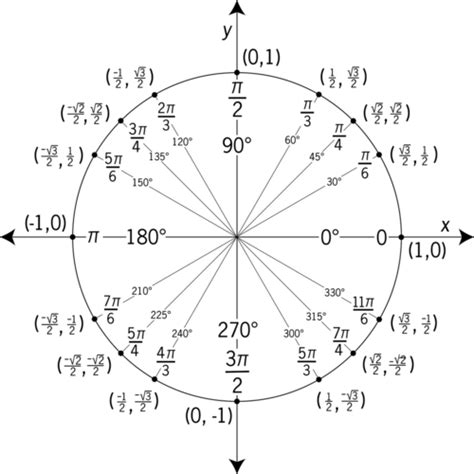
In conclusion, the unit circle is a powerful tool for visualizing and calculating trigonometric relationships. Using a unit circle chart printable can help you to better understand the unit circle and to calculate the values of the trigonometric functions for specific angles. The unit circle has several applications in various fields, including physics, engineering, and computer science. By understanding the unit circle and its properties, you can gain a deeper appreciation for the beauty and complexity of mathematics.
Final Tips and Recommendations
Here are some final tips and recommendations for working with the unit circle: * Use a unit circle chart printable to visualize the relationships between the trigonometric functions. * Practice calculating the values of the trigonometric functions for specific angles. * Apply the unit circle to real-world problems and examples. * Continue to learn and explore the properties and applications of the unit circle.Unit Circle Image Gallery
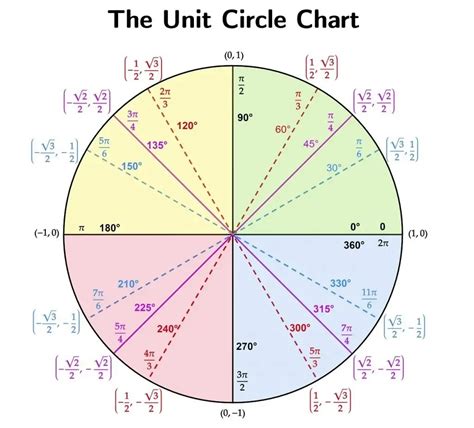
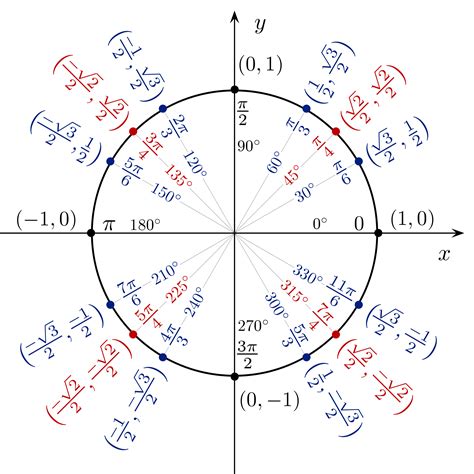
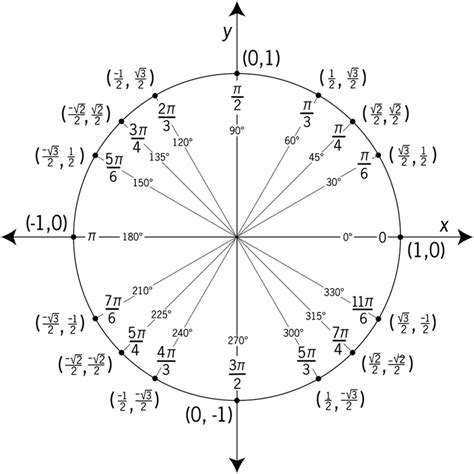
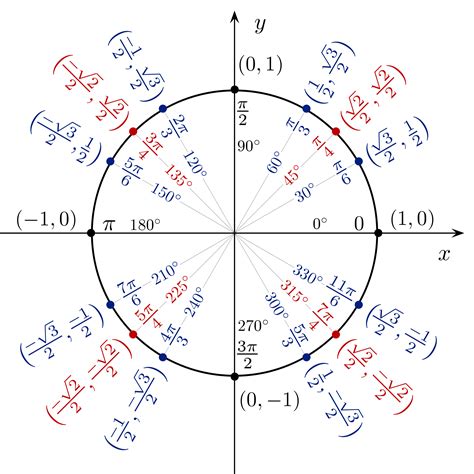

What is the unit circle?
+The unit circle is a circle with a radius of 1 unit, centered at the origin of a coordinate plane.
What are the properties of the unit circle?
+The unit circle has several key properties, including symmetry about the x and y axes, a radius of 1 unit, and the definition of the trigonometric functions as the ratios of the lengths of the sides of a right triangle.
How do I use a unit circle chart printable?
+To use a unit circle chart printable, start by identifying the angle for which you want to calculate the trigonometric functions. Next, find the corresponding point on the unit circle and read off the x and y coordinates. Finally, use the x and y coordinates to calculate the sine, cosine, and tangent of the angle.
What are the applications of the unit circle?
+The unit circle has several applications in various fields, including physics, engineering, and computer science. Some of the most important applications include calculating the trajectories of projectiles, modeling the motion of objects in circular orbits, and analyzing the vibrations of mechanical systems.
How do I create a unit circle chart printable?
+To create a unit circle chart printable, start by drawing a circle with a radius of 1 unit, centered at the origin of a coordinate plane. Next, draw the x and y axes and label the points on the circle where the axes intersect. Then, calculate the x and y coordinates of points on the circle for common angles, such as 30, 45, 60, and 90 degrees. Finally, use the x and y coordinates to calculate the sine, cosine, and tangent of the angles and create a chart that shows the values of the functions.
We hope this article has provided you with a comprehensive understanding of the unit circle and its properties. If you have any further questions or would like to learn more about the unit circle, please don't hesitate to comment or share this article with others. Additionally, you can explore more resources and tutorials on the unit circle to deepen your understanding of this fundamental concept in mathematics.
